
Spiritualism, religion and mathematics in the Victorian period
By Sylvia Nickerson
In 1884 the English schoolteacher Edwin Abbott published Flatland: A Romance of Many Dimensions. This book, a social satire, also explores the mathematical concept of dimensionality. Abbott’s characters imagine what it might be like for creatures of one dimension to communicate with creatures of higher or lower dimensions. A major theme is how differently dimensional creatures could perceive and believe in creatures of alternately dimensional worlds. Abbott’s book can be read as a commentary on science and faith in the Victorian period, as his characters are conflicted between their desire to believe and their want of rigorous intellectual explanation, and material proof for their belief. Flatland describes a territory familiar to nineteenth-century British society, in which the project of reconciling their spirituality with the assimilation of contemporary scientific (and mathematical) theory into one holistic worldview was an ongoing and common concern.
Late nineteenth-century British culture was somewhat preoccupied with the presence of ghosts. Conjuring spirits at séances was a popular pastime, with the exploits of some spiritualists, such as the medium Henry Slade, the fodder of press gossip and celebrity. Communicating with spirits became of deep interest to some scientists, including the physicist William Crookes and the naturalist Alfred Russel Wallace, who debated their peers about aberrant physical phenomena and whether certain observations confirmed the reality of spirits or not.

Talking boards, also known as Ouija boards, automatic writing, knot-tying, levitation and other experiments designed to prove the interference of spirits with the physical world, flourished in Britain at the end of the century. Several proponents of the new Spiritualist movement used theoretical evidence from nineteenth-century geometry to both justify the reality of their otherworldly explorations and to form methods with which to enter into transcendent realms.
The mathematical world was changed in 1832 upon discovering that Euclidean geometry, that classical description of space, in which triangles have 180 degrees and parallel lines extend to infinity, was only one possible description of three-dimensional space. As it turned out many other geometries were possible. In hyperbolic geometry, the angles of a triangle total less than 180 degrees, and parallel lines diverge at infinity. In elliptic geometry, the angles of a triangle add to more than 180 degrees and all lines intersect. These were some of the nineteenth-century discoveries that fundamentally changed mathematics, bringing about a new modernist approach to the discipline.
The discovery of multiple geometries was one of the ideas that lead to a fundamental re-think about how space itself can be defined mathematically. In 1854 German mathematician Bernhard Riemann generalized the concept of spatial measurement in his work Ueber die Hypothesen welche der Geometrie zu Grunde liegen. Riemann’s new mathematical definition of measurement opened many more possibilities for the description of space, including the possibility of multidimensional geometries; mathematical descriptions of space greater than three dimensions.
From the mid-century onwards, multidimensional geometry and non-Euclidean geometry were debated, and their implications upon human experience became of popular interest. Mathematically defined, but fundamentally abstract, geometrical spaces left plenty of room for mystical or spiritual believers to add new meanings to these ideas. In 1880 the mathematics teacher Charles Howard Hinton published an article entitled “What is the Fourth Dimension?” in which he outlined a method for visualizing and interacting with the ethereal world defined for him by the mathematical fourth dimension. Exploring this world held a certain moral zeal for Hinton, who sought out the mental discipline that envisioning the fourth dimension would demand.
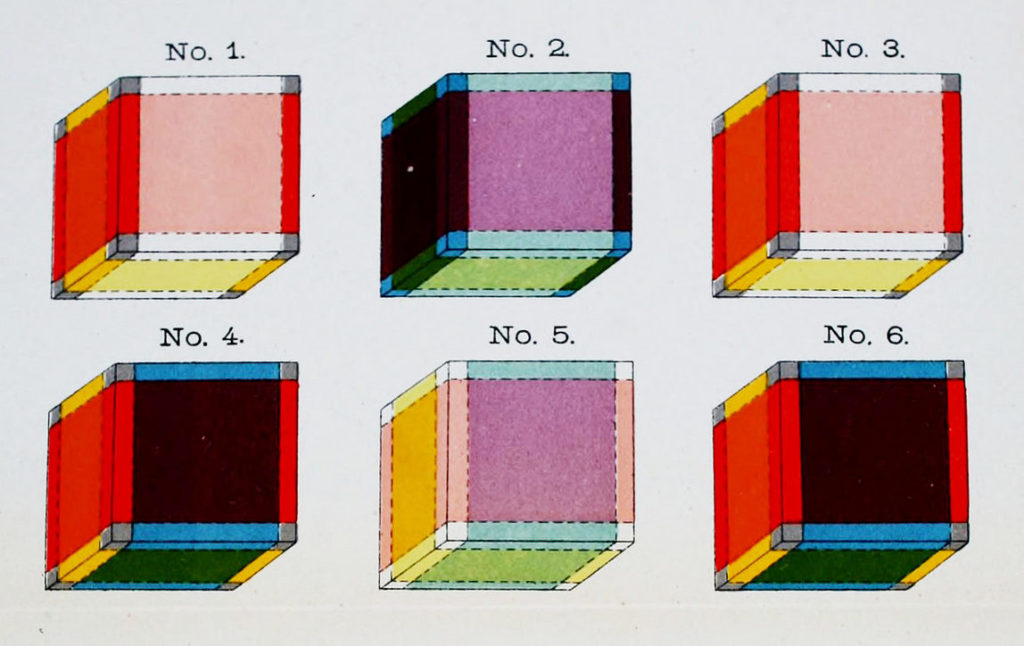
Hinton created a method of visualization that involved a mental device he called the tesseract. Imagine a cube subdivided into many smaller cubes, each coded by either a colour or a number. Through a visualization exercise, the “shadows” of four-dimensional objects could be observed as their intersections were imagined to pass through the tesseract. In this way, higher space could be perceived, if incompletely. Hinton further expanded his fourth-dimensional speculations in several science fiction books including Scientific Romances (1884-1886) and An Episode on Flatland (1907).
The German physicist Karl Zöllner also explored the connection between four-dimensional space and Spiritualism in several books toward the century’s end. In Transcendental Physics (1878) Zöllner describes séance experiments in which coins are unaccountably moved outside of sealed boxes. If the spiritual dimension overlaps with our own, then could spirits move objects in our dimension, at their will? Zöllner used the geometrical work of Riemann and Karl Gauss to give a theoretical and scientific justification for his Spiritualist belief that just as mathematical objects in the fourth dimension can penetrate the third dimension, spirits can pass through our space from their esoteric space when they will.

In 1884 the English schoolteacher Edwin Abbott published Flatland: A Romance of Many Dimensions. This book, a social satire, also explores the mathematical concept of dimensionality. Abbott’s characters imagine what it might be like for creatures of one dimension to communicate with creatures of higher or lower dimensions. A major theme is how differently dimensional creatures could perceive and believe in creatures of alternately dimensional worlds. Abbott’s book can be read as a commentary on science and faith in the Victorian period, as his characters are conflicted between their desire to believe and their want of rigorous intellectual explanation, and material proof for their belief. Flatland describes a territory familiar to nineteenth-century British society, in which the project of reconciling their spirituality with the assimilation of contemporary scientific (and mathematical) theory into one holistic worldview was an ongoing and common concern.

Sylvia Nickerson is a sessional lecturer in the history of mathematics at the University of Toronto. She previously worked on the editorial project The Correspondence of John Tyndall and the multidisciplinary project Science and Religion: Exploring the Spectrum as a postdoctoral researcher in history of science at York University from 2014-2017.

